The Fastest Groth16 CPU Prover in the World

RabbitSNARK is up to 2× faster than RapidSNARK, making it the fastest Groth16 CPU prover in the world today.

Intro

In the deep learning world, models are typically written in Python and then compiled at runtime into optimized code for the target machine. In contrast, Groth16 provers in the ZK domain have traditionally been implemented directly in languages like C++ (RapidSNARK, ICICLE-Snark), Go (Gnark), and Rust (circom-compat).

RabbitSNARK overcomes these limitations by being the first to apply compiler techniques from deep learning to ZK proving. This approach achieves state-of-the-art Groth16 CPU proving performance across a wide range of platforms—including Linux and macOS, as well as x86 (AMD) and ARM (Graviton, Apple Silicon).

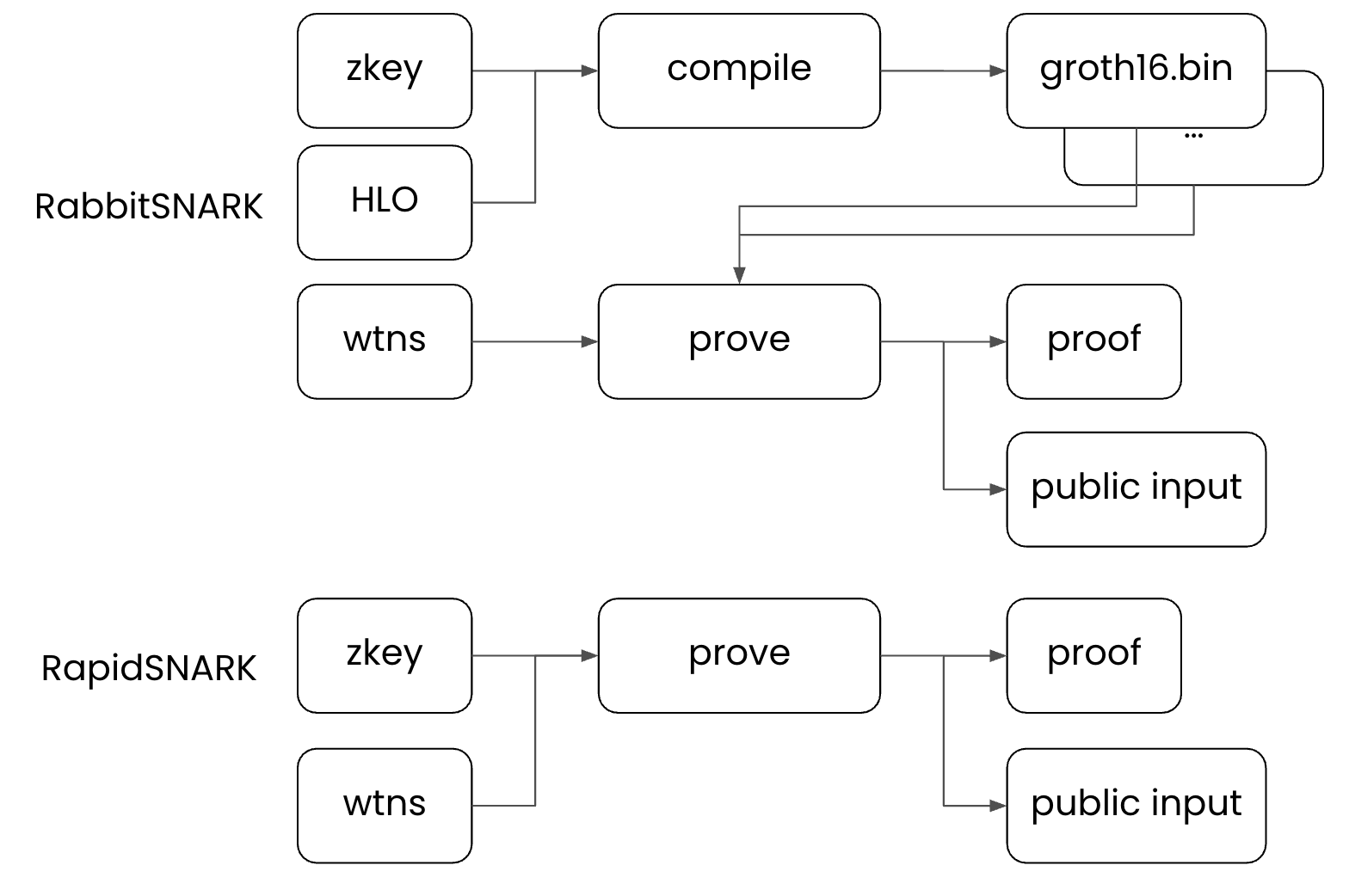
The key differentiator of RabbitSNARK is its two-stage design: unlike traditional Groth16 provers that generate proofs in a single step given the zkey and wtns, RabbitSNARK separates this into a Compile phase and a Prove phase. This approach allows it to generate circuit-specific, highly optimized code that performs proof generation efficiently.

Background

Our design is inspired by XLA and MLIR. For readers who may be unfamiliar, here's a brief introduction to these concepts.

MLIR (Multi-Level Intermediate Representation)

MLIR is a subproject of LLVM.

LLVM IR is a general-purpose intermediate representation, but it lacks domain-specific knowledge, making specialized optimizations difficult to express.

In the deep learning world, frameworks started developing their own domain-specific compilers or languages to speed up training and inference. However, this approach brings several problems:

• Software fragmentation: Different domains and frameworks use different IRs or compilers, reducing interoperability.
• Reduced reusability: Common logic gets reimplemented in each system.
• Limited hardware portability: Weak integration with general-purpose compilers makes supporting heterogeneous hardware challenging.

To address these issues, Chris Lattner (creator of LLVM) proposed MLIR, which reuses the LLVM infrastructure while supporting domain-aware optimizations and flexible targeting of diverse hardware.

HLO (High Level Operation)

HLO is an intermediate representation used in XLA. When users write deep learning models in Python, they are first transformed into HLO, which can then be lowered to MLIR for machine-dependent optimization.

As mentioned earlier, in deep learning, models are defined in Python and then compiled for the target environment. Similarly, in RabbitSNARK's current PoC stage, we use HLO to describe the Groth16 proving scheme.

The entire Groth16 proving scheme can be expressed in roughly 80 lines of HLO code (including whitespaces), making it highly readable and concise.

One key feature of HLO is that it explicitly specifies each operation's input/output buffer sizes and execution order. This enables the compiler to generate an optimal execution schedule that considers memory usage—that is, it can plan the most efficient order of instructions given the available memory constraints.

Example Code

Below is an example of the QAP portion of the Groth16 prover expressed in HLO:

%Az = bn254.sf[8388608] dot(%A, %z.in_mont)
%Bz = bn254.sf[8388608] dot(%B, %z.in_mont)
%Cz = bn254.sf[8388608] multiply(%Az, %Bz)

%a.poly = bn254.sf[8388608] fft(%Az, %ifft_twiddles), fft_type=IFFT, fft_length=8388608, fft_do_bit_reverse=false, control-predecessors={%Cz}
%b.poly = bn254.sf[8388608] fft(%Bz, %ifft_twiddles), fft_type=IFFT, fft_length=8388608, fft_do_bit_reverse=false, control-predecessors={%Cz}
%c.poly = bn254.sf[8388608] fft(%Cz, %ifft_twiddles), fft_type=IFFT, fft_length=8388608, fft_do_bit_reverse=false

%a.poly_x_twiddles = bn254.sf[8388608] multiply(%a.poly, %twiddles)
%b.poly_x_twiddles = bn254.sf[8388608] multiply(%b.poly, %twiddles)
%c.poly_x_twiddles = bn254.sf[8388608] multiply(%c.poly, %twiddles)

%a.evals = bn254.sf[8388608] fft(%a.poly_x_twiddles, %fft_twiddles), fft_type=FFT, fft_length=8388608, fft_do_bit_reverse=false
%b.evals = bn254.sf[8388608] fft(%b.poly_x_twiddles, %fft_twiddles), fft_type=FFT, fft_length=8388608, fft_do_bit_reverse=false
%c.evals = bn254.sf[8388608] fft(%c.poly_x_twiddles, %fft_twiddles), fft_type=FFT, fft_length=8388608, fft_do_bit_reverse=false

%h.evals.tmp = bn254.sf[8388608] multiply(%a.evals, %b.evals)
%h.evals = bn254.sf[8388608] subtract(%h.evals.tmp, %c.evals)

XLA (Accelerated Linear Algebra)

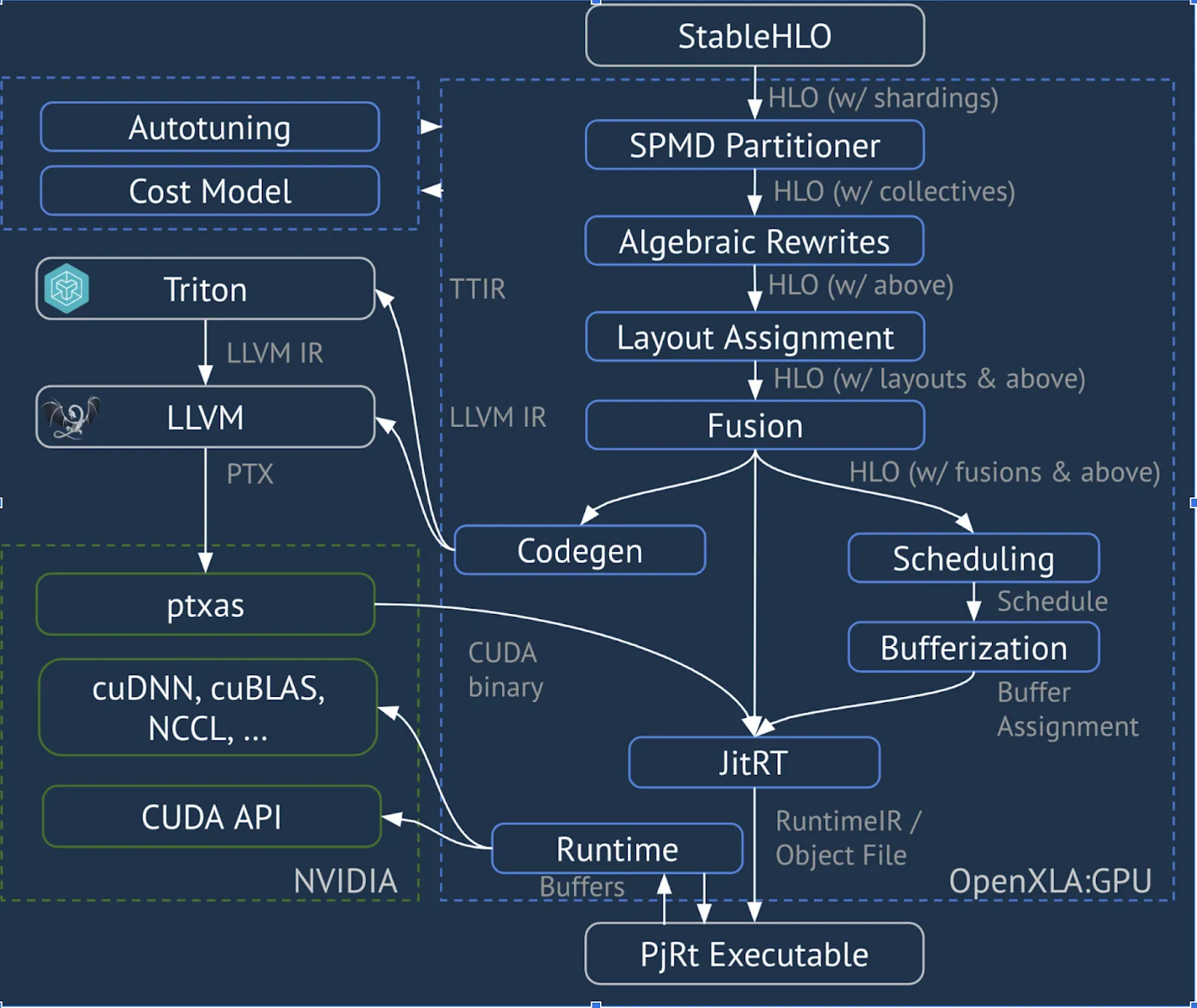
XLA takes the HLO representation described above as input and applies a variety of optimization passes. Key optimization stages include:

• SPMD Partitioner: Efficiently splits the model across multiple devices
• Algebraic Rewrites: Simplifies and rewrites expressions
• Layout Assignment: Optimizes memory layouts
• Fusion: Combines multiple kernel calls to reduce runtime overhead

Through these passes, XLA generates machine-independent, optimized HLO code.

The optimized HLO is then lowered to machine code using backends such as Triton and LLVM, making it executable on the target hardware.

ZKX, ZKIR, RabbitSNARK

ZKX is a specialized ZK runtime compiler developed by Fractalyze, modeled after XLA.

Just as XLA abstracts over different machine architectures (CPU, GPU, TPU) to generate high-performance code, ZKX aims to automatically generate efficient ZK proving code across diverse hardware environments.

A core component of ZKX is ZKIR.

Based on MLIR, ZKIR is a domain-specific intermediate representation designed to support domain-aware optimizations and lowering.

Much like how MLIR defines various domain-specific dialects to enable generic optimizations and target-specific code generation, ZKIR abstracts ZK proving computation patterns and transforms them into optimized machine code.

RabbitSNARK is a Groth16 CPU prover built using ZKX and ZKIR.

It compiles Groth16 proving logic, expressed in ZKIR, into highly optimized code for a variety of machine architectures—enabling platform-independent, high-performance proving.

Benchmark

The circuits used for benchmarking were sourced from ICICLE-Snark. We replaced the Keyless circuit with the RISC0 circuit.

According to ICICLE-Snark's official benchmark results, RapidSNARK delivers highly competitive performance on CPUs like the Ryzen 9 9950X and i9-13900K.

For this reason, we chose RapidSNARK as the primary comparison target.

We also plan to publish our benchmarking scripts to ensure that results can be fully reproduced by anyone.

Results

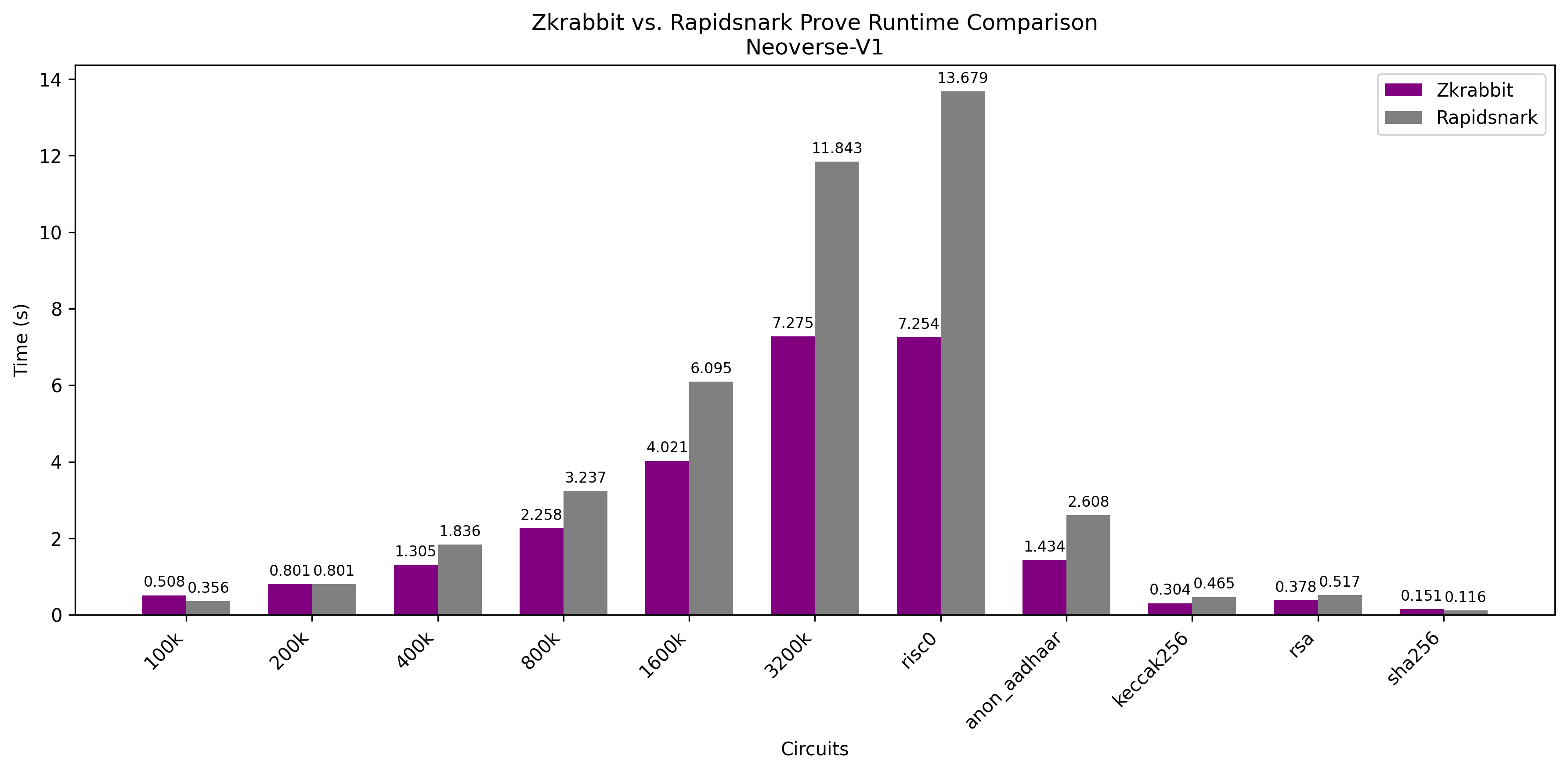
AWS c7g.8xlarge

AWS c7a.8xlarge

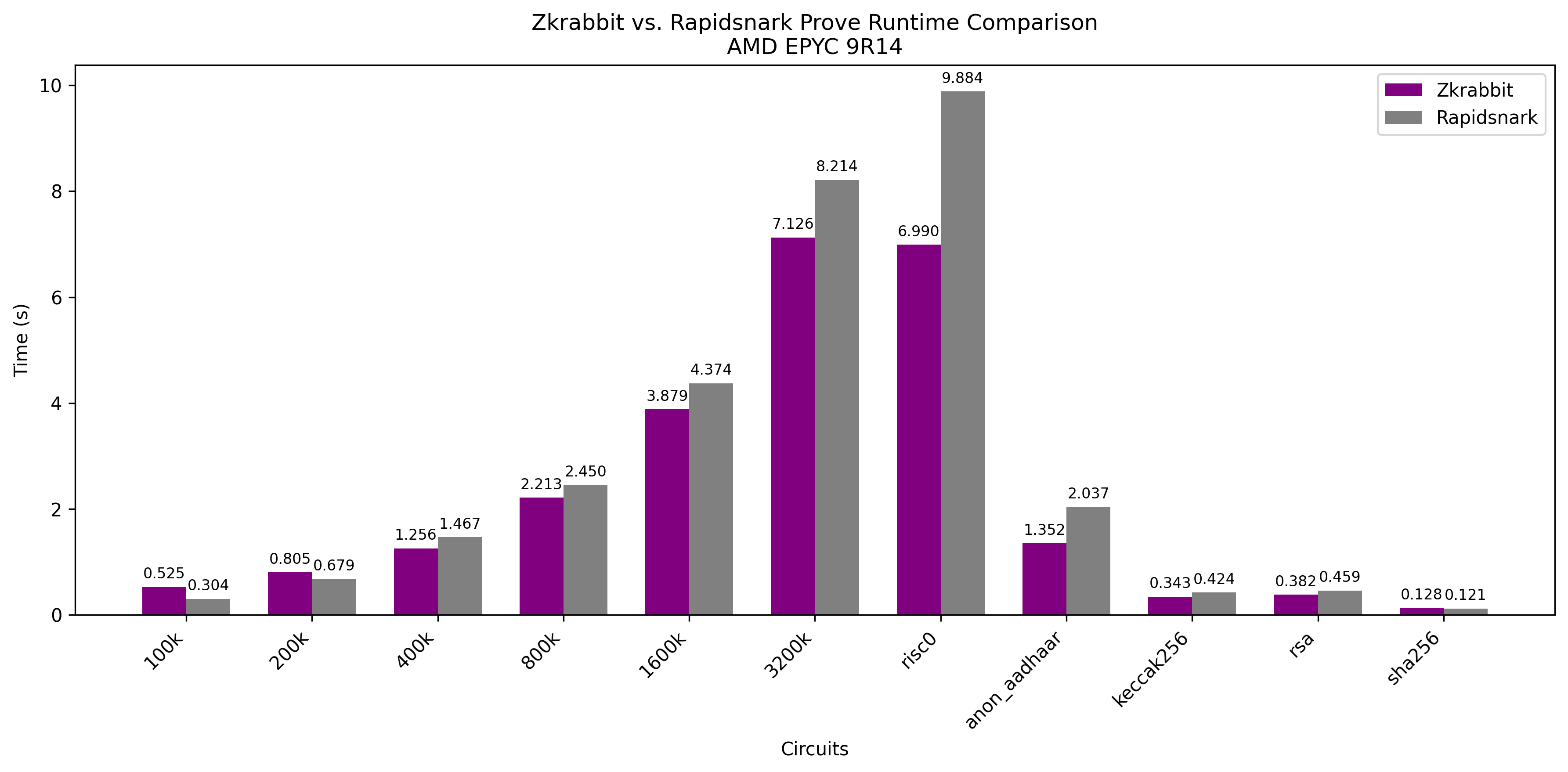
M4 Pro

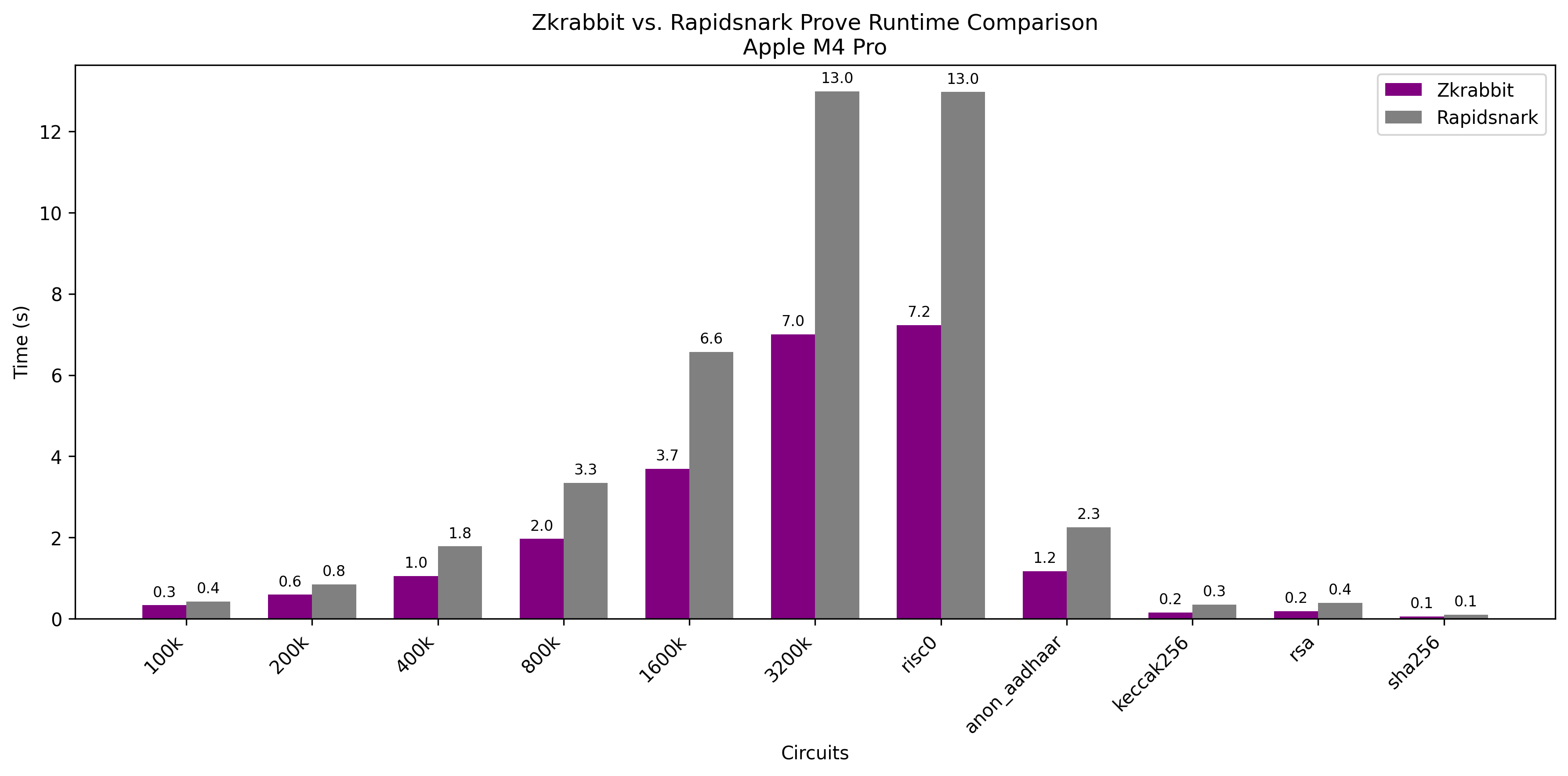
Explanation

Machine-independent Stable Performance

Benchmark results on comparable AWS c7-series instances show that RabbitSNARK delivers highly consistent performance across different machines.

This is especially important considering that AWS c7g instances use Graviton (ARM) processors, which are 20~40% cheaper than equivalent x86 instances.

In production, we care not only about raw performance but also about cost. If a prover's performance varies significantly between machines and requires manual tuning for each environment, it becomes a serious productivity bottleneck.

The reason RapidSNARK performs worse on ARM-based instances like c7g or M4 Pro is:

• RapidSNARK uses nasm with manually written, CPU-specific optimized assembly, such as mul.asm.ejs.
• However, there is no dedicated ARM assembly implementation, so it can't deliver optimal performance on ARM processors.

In contrast, RabbitSNARK uses an MLIR/LLVM-based compiler that automatically detects the machine architecture and generates optimized code.

This enables consistently high performance across platforms without requiring architecture-specific tuning.

Performance Breakdown

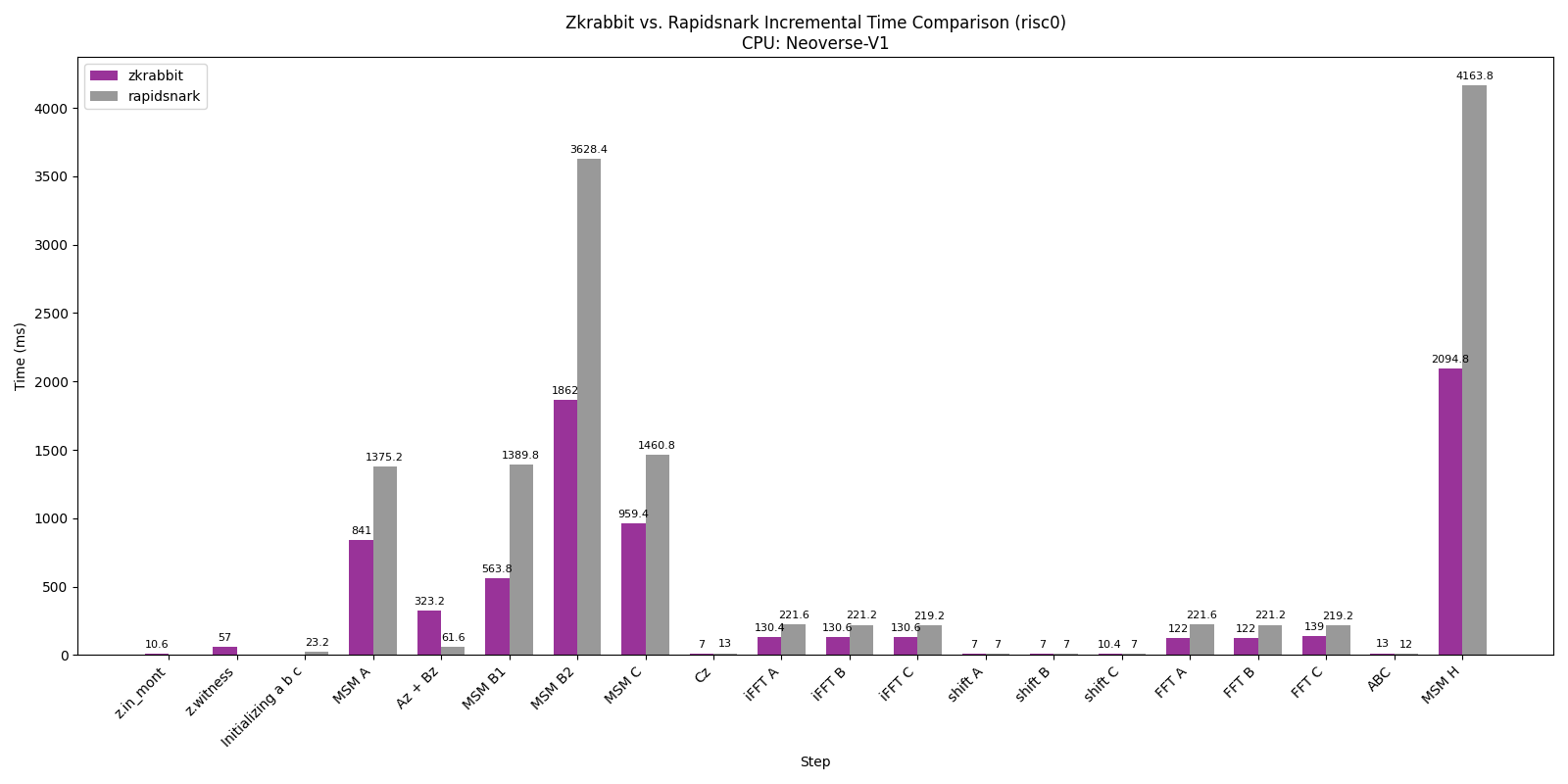
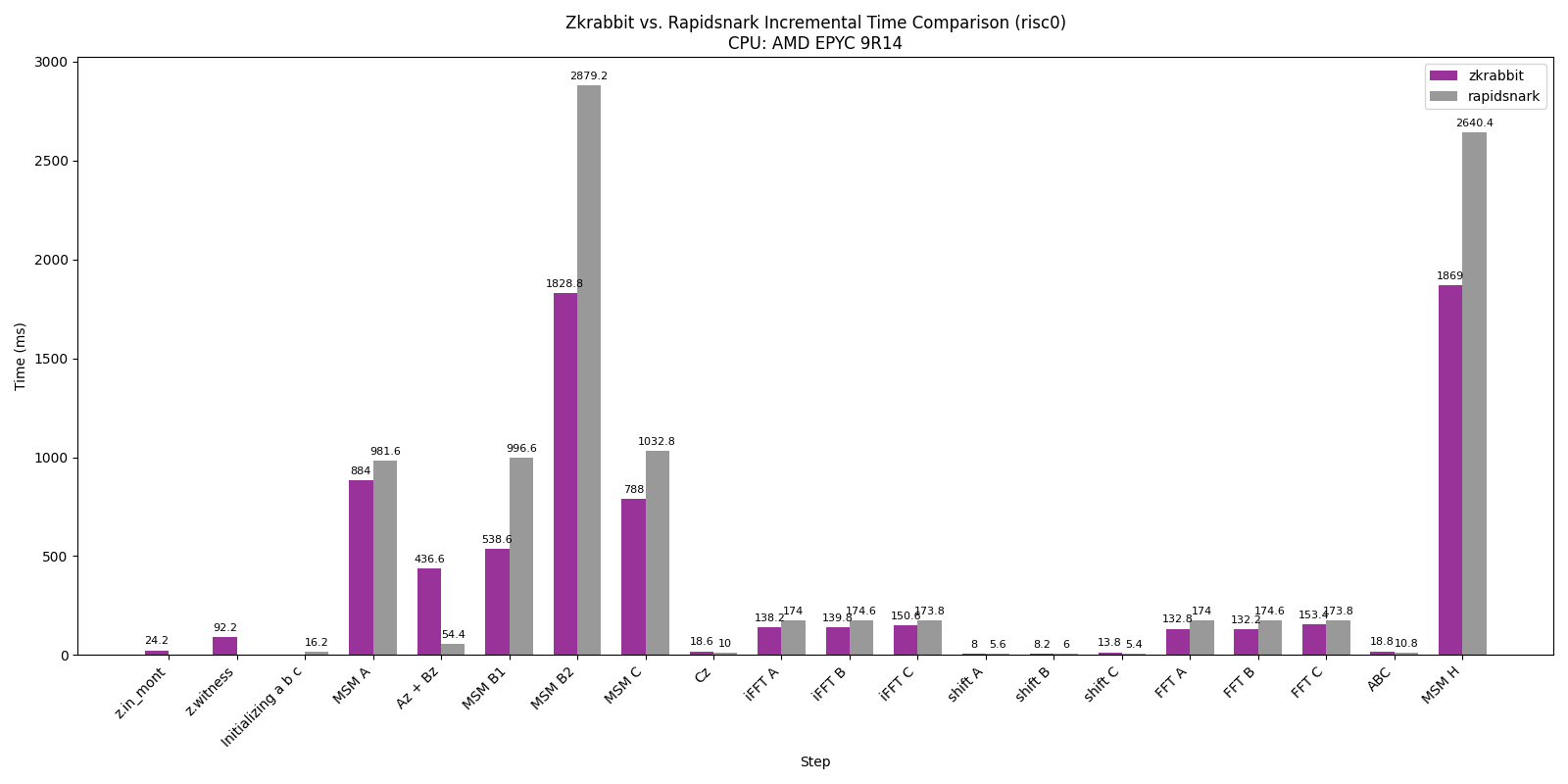
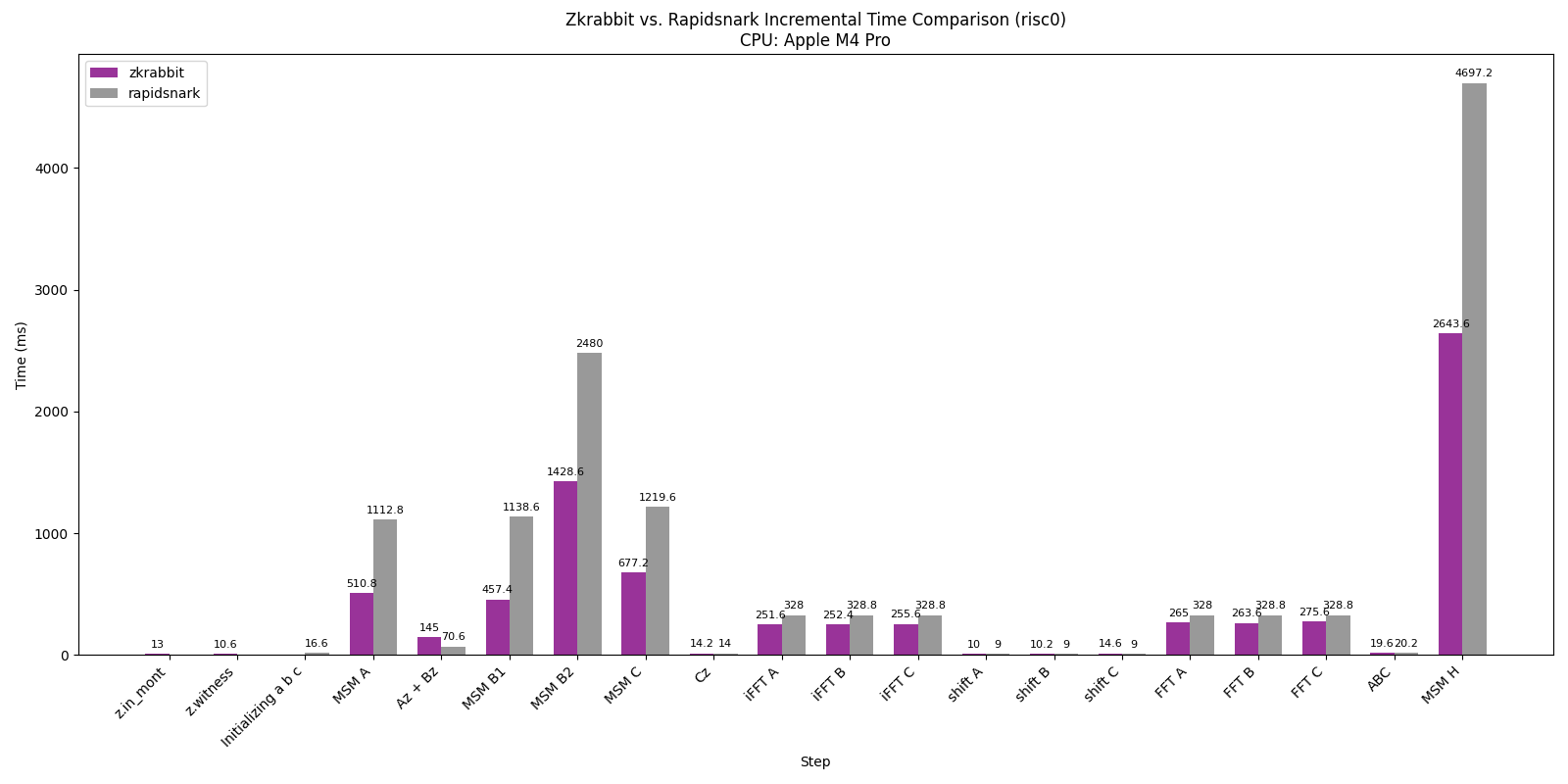
These charts show a detailed breakdown of the RISC0 circuit benchmark across different machines.

For both AMD and ARM environments — except for the Az + Bz section — RabbitSNARK is approximately 2× faster than RapidSNARK.

Analysis

Why is it faster?

Term-based MSM Parallelization

The complexity of MSM is determined by the window bit size, following Pippenger's algorithm.

For example, handling an MSM of size $2^{20}$ typically results in about 16 windows.

If you use window-based parallelism like RapidSNARK does, it becomes difficult to fully utilize all CPU cores.

For instance:

• An M4 MacBook has 14 cores (10 Performance cores + 4 Efficiency cores).
• An AWS c7.8xlarge instance offers 32 cores.

With only 16 windows to work with, the number of parallel tasks is limited and can't match the available cores, leading to underutilization.

RabbitSNARK addresses this limitation by adopting a term-based parallelization strategy.

By partitioning MSM terms independently and assigning them to threads, RabbitSNARK can fully leverage all available CPU cores.

This approach delivers excellent scaling performance across machines with varying numbers of cores.

Ingonyama SOS

In modular arithmetic, the most expensive operation is multiplication.

To handle this efficiently, the Montgomery Multiplication technique is used. This technique can be implemented using one of the two common strategies: [CIOS] or [SOS].

RabbitSNARK adopts the SOS approach and incorporates the recent optimization by the Ingonyama team.

If you wanted to apply the same optimization in RapidSNARK, you would need to manually write the assembly code using ffiasm.

In contrast, RabbitSNARK is written in MLIR, allowing LLVM to automatically generate architecture-optimized assembly code for each target machine.

Algebraic Rewrites

RabbitSNARK implements algebraic rewrites in its compiler pass to automatically detect computational patterns and rewrite them into more efficient forms.

For example, extension field squaring is optimized like so:

In the BN254 curve's extension field $\mathbb{F}_{p^2}$, the chosen non-quadratic residue is -1.

That is, $\beta^2 = -1$, and any element can be expressed as:

$$x_0 + \beta x_1 \in \mathbb{F}_{p^2}, \quad x_0, x_1 \in \mathbb{F}_p$$

Additionally, when $\beta^2 = -1$, the squaring operation in $\mathbb{F}_{p^2}$ expands as:

$$(x_0 + \beta x_1)^2 = x_0^2 + \beta^2 x_1^2 + \beta(2x_0x_1) = x_0^2 - x_1^2 + \beta(2x_0x_1)$$

This means that when $\beta^2 = -1$, an algebraic rewrite can replace the naive multiplication $\beta^2 \times y$ with a simple negation of $-y$ instead.

Thus, algebraic rewrites allow developers to write generic, readable code and rely on the compiler to apply these optimizations automatically.

This kind of algebraic rewrite is especially crucial for compute-heavy operations like the S-box in [Poseidon2 hash].

Bit Reversal

By leveraging Jordi's Trick, the computation of the polynomial $h(X)$ requires performing the following pattern three times:

• IFFT → elementwise multiplication with a constant → FFT

In this process, Bit Reversal operations are normally needed after the IFFT and before the FFT stages.

However, if the constant vectors are preprocessed and stored in a bit-reversed form ahead of time, these Bit Reversal steps can be entirely eliminated at runtime.

This optimization can be performed at compile time.

Because Bit Reversal is an involution (like negation or inversion), and the elementwise multiplication with a constant can be rewritten ahead of time, the compiler can precompute these transformations to remove unnecessary runtime work.

Precomputing Constants

In Groth16, there are three types of constants that can be precomputed at compile time:

• FFT twiddles
• Inverse FFT twiddles
• Twiddles used in Jordi's Trick

Typically, as in RapidSNARK, these constants are computed at runtime and cached for reuse when the same circuit is proved multiple times.

However, because RabbitSNARK separates the compile phase, these constants can be calculated ahead of time during compilation and embedded directly into the generated code.

This approach reduces runtime overhead and further optimizes proof generation speed.

Why is it slower?

Sparse Matrix Vector Multiplication

The Az + Bz section is the only part where RabbitSNARK is slower than RapidSNARK.

When parallelizing SpMV(Sparse Matrix Vector multiplication) with multiple threads, MLIR often use a row-based partitioning strategy.

However, the distribution of rows per thread is highly imbalanced, severely reducing parallel efficiency.

To solve this, you would need to partition not by rows, but by NNZ (Number of Non-Zero Elements) to ensure balanced work across threads.

In this PoC, we determined that this section was not the main bottleneck for Groth16 as a whole, so optimizing it was deprioritized for now.

However, we expect that applying this optimization in the future will enable the Az + Bz stage to outperform RapidSNARK as well.

Future Works

Groth16 on GPU

XLA was originally designed as a GPU / TPU-optimized framework.

RabbitSNARK's Groth16 CPU PoC was intended as a starting point for analyzing and tackling the cost and performance challenges of proof generation on GPUs.

Now that we've validated these optimizations on CPU, our next goal is to extend this baseline into a high-performance proving system that is vendor-independent (AMD, Nvidia) and GPU-architecture-agnostic.

Groth16 on FPGA / ASIC / Mobile / Web

Just as XLA supports a wide range of hardware targets (CPU, GPU, TPU) through a single abstract program representation (HLO), RabbitSNARK aims to provide a backend abstraction that can target FPGA, ASIC, Mobile, and Web environments for Groth16 proving.

The biggest advantage of this approach is that developers only need to maintain a single HLO definition.

Once the proving algorithm is expressed in HLO, the compiler can automatically generate optimized code tailored for each target architecture.

Distributed Groth16

As far as we know, the only system that maintains Groth16's structure while enabling distributed proof generation is DIZK.

However, DIZK suffers from significant communication overhead due to its approach of distributing FFT computations.

To overcome these limitations, we plan to adopt SPMD as supported in XLA.

SPMD enables the compiler to generate programs that apply both Data Parallelism and Model Parallelism at compile time, using hints provided by the developer.

Through this approach, we are designing a new method to efficiently generate Groth16 proofs in distributed environments.

ZK in Python

In deep learning, models are typically written in Python, and that same code can be used directly in production.

In contrast, the ZK space today mostly relies on Rust to implement Proving Schemes.

If ZK code could similarly be written in Python, it would offer the major advantage of maintaining consistency between the spec and production code.

Proving Scheme Extension

Currently, RabbitSNARK offers a minimal set of opcodes required to support Groth16.

Just as XLA defines and provides a wide range of operation semantics, our plan is to define a ZK-specific opcode specification and incrementally expand it.

This will enable the platform to support not only Groth16 but also a variety of ZK proving schemes—all implemented and optimized on top of the same IR foundation.

Conclusion

Fractalyze's vision is to "Accelerate a Verifiable World Where Proof Replaces Trust." We aim to achieve this not by relying on trust-based assumptions, but by building systems secured through mathematically verifiable ZK Proofs.

In recent years, the pace of advancement in ZK technology has been extraordinary—far beyond what was imaginable just a decade ago.

However, cost and performance challenges remain, and we believe that solving these will make ZK a core technology for addressing trust problems far beyond blockchain alone.

At Fractalyze, we approached these challenges from first principles, and this result is a milestone achieved in just five months.

Of course, there are still many problems left to solve, but we believe that 2025 will see even more breakthroughs and accelerated innovation.

Thank you.